Multi-valued variables in Python

Can a variable have more than one value? Of course the answer is no. But it sure would be useful in a lot of situations.

One example is when calculating square roots. math.sqrt(4) gives us the answer 2 but that's not fully accurate. -2 is also a correct answer. The square root function needs to return two correct answers. Following this logic, the equation sqrt(4) + 2 has two correct answers as 4 and 0.

Now, write a program to give all possible correct answers for the following equation: sqrt(sqrt(sqrt(4) + 2) + 2) (there are 5 correct answers in all)

A Naive Solution

A naive solution would be to think that we can just represent multiple values using a list (or tuple or set). So, our sqrt function would be written this way (for the purpose of this article, lets disregard negative numbers)

import math

def sqrt(n):
    if n < 0:
        return []
    if n == 0:
        return [0]
    val = math.sqrt(n)
    return [-val, val]

But now we have a problem, because a code like sqrt(4) + 2 will stop working once sqrt returns a list instead of a number. Instead we will need to do something like this

vals = [root+2 for root in sqrt(4)]

Now we can see how this approach will explode in complexity when we want to do a longer and more complicated calculation like sqrt(sqrt(sqrt(4) + 2) + 2)

There is a better way.

Monads

If you have been following Playful Python since the beginning, you would have encountered our first series of articles on functional programming where we introduced the concept of monads. Below is the link, I'd suggest quickly going over the article once, as we will be using that concept here

Introducing Monads in Functional Programming

Monads have a reputation as being a very complicated aspect of functional programming. In this article we demystify them and learn how to apply monads in our code

Playful PythonSiddharta Govindaraj

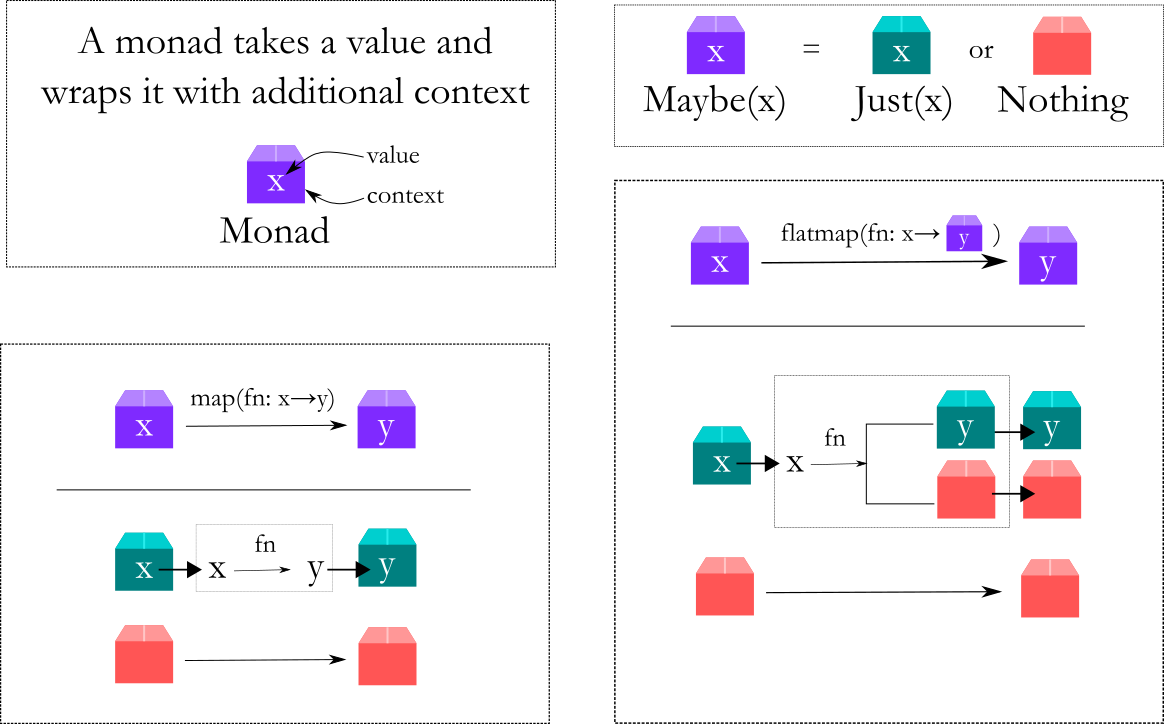
To quickly summarise:

• Monads are objects that are wrappers around the actual value
• The monad wrapper stores additional data besides the actual value, such as success/failure state or logs of operations or it could be anything else
• The monad wrapper also contains two standard methods called map and flatmap that are used to chain successive operations one after the other
• At the end of a sequence of operations we can unwrap the monad to get the final value of the computation, plus any of the additional data stored in the monad

Multi-value Monad

Let us now take a look at how we can create a multi-value monad. In functional programming languages like Haskell, regular lists data type is automatically implemented as monads, but this is Python so we will derive it from scratch.

We saw in the example above that using a list to represent multiple values breaks subsequent operations on that result. Example, sqrt(4) + 2 will not work anymore.

A monad has special methods map and flatmap that can be used to sequence further computation. Maybe we can use that to solve our problem? Let's see how that can work.

First, we will create our class. It will accept an Iterable containing all the values that we want to wrap. We will store this in a set since that will get rid of duplicate values

class MultiValue:
    def __init__(self, values):
        self.values = set(values)

Now we need to implement the map function. The map function is used to apply a function to our value. Since our monad has a set containing multiple values, we need to apply that function to each value in the set.

So if we have a monad with the values {-2, 2} and we want to do the operation + 2 then we need to do that operation to each value, giving an output monad with the values {0, 4}

    def map(self, fn):
        out = {fn(val) for val in self.values}
        return MultiValue(out)

Finally, flatmap. This method is used when the function to apply itself returns a monad as output. Example sqrt(sqrt(4) + 2). The inner computation gives us a set of values {0, 4}. Then when we apply the sqrt on this

• First value sqrt(0) gives a monad containing {0} as the output
• While sqrt on the second value sqrt(4) gives {2, -2} as output

To get the final output, we need to flatten all these individual results and get {0, 2, -2} as the final result.

This is what the flatmap function needs to do. Here is the code

    def flatmap(self, fn):
        out = (fn(val).values for val in self.values)
        return MultiValue(chain(*out))

The line chain(*out) flattens the iterable. If you are not familiar with that syntax, take a look at our Python Lab that explains how it works

Python Lab: How to flatten a list

Today, we ask: How do you flatten a list in Python?

Playful PythonSiddharta Govindaraj

Full code for the monad

from itertools import chain

class MultiValue:
    def __init__(self, values):
        self.values = set(values)
        
    def map(self, fn):
        out = {fn(val) for val in self.values}
        return MultiValue(out)
        
    def flatmap(self, fn):
        out = (fn(val).values for val in self.values)
        return MultiValue(chain(*out))

Solving the math problem

Now that we have the monad ready, we can solve the math problem. First, sqrt function returns multiple values, so we will wrap the multiple values in our monad before returning it

import math

def sqrt(n):
    if n < 0:
        return MultiValue(set())
    val = math.sqrt(n)
    return MultiValue({-val, val})

Now we define the + 2 function. This is an ordinary function that takes a number as input and returns a number as output. No monads here.

# you can also use lambda or partial instead
def plus_2(x):
    return x + 2

Finally, we sequence the operations. When we want to apply plus_2 function we use map. When we want to apply the sqrt function which returns a monad, we use flatmap.

out = (sqrt(4)         # square root 4
       .map(plus_2)    # add 2
       .flatmap(sqrt)  # sqrt the result
       .map(plus_2)    # add 2 again
       .flatmap(sqrt)) # final sqrt
print(out.values) # all 5 correct answers

Isn't it beautiful?

We can sequence the operations one after the other without concerning with the fact that some steps will return multiple values. All operations will work fine and we will get all five correct answers in the end.