Introducing Monads in Functional Programming

A monad is just a monoid in the category of endofunctions, what's the problem?

The quote above is from James Iry in his very funny article "Brief, Incomplete and Mostly Wrong History of Programming Languages". It is a parody of how functional programming has a lot of mathematical jargon which turns off a number of regular programmers. Right on top of the list is the explanation of the monad.

In this article, we are going to learn about monads from a very practical perspective, skipping the math.

The Scenario

We start with two functions inverse and inc which return the inverse and increment respectively

def inverse(x):
    return 1/x
    
def inc(x):
    return x + 1

If we want to do these two operations in sequence, we can compose them together.

fn = compose(inverse, inc)
fn(10) # 1.1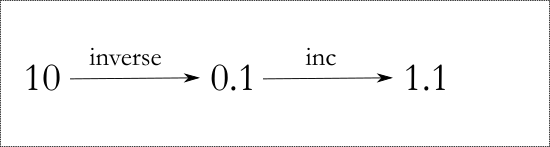

However, the code blows up when x is zero.

How do we handle the case when x is zero? Normally in object-oriented programming we would throw an exception, but in functional programming that would make the function impure. In order to make a pure function implementation, all information – including errors – should be in the returned output.

Perhaps we can modify the inverse function to return the success/failure status along with the output

def inverse(x):
    if x == 0:
        return (False, None)
    return (True, 1/x)

But now that we have changed the function signature this way, we can no longer compose normally.

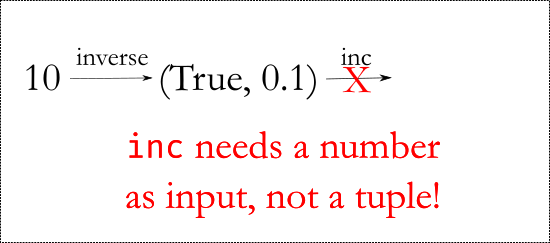
Combining the two functions

We are going to create a function called map to help us compose these two functions together

def map(val, fn):
    success, output = val
    if not success:
        return val
    return (True, fn(output))

This function takes in the success/failure tuple as the first parameter and the function to compose with as the second parameter.

It will check the status of the tuple. If it is empty, then it will return the same empty tuple without calling the second function. Otherwise it will take the output value in the tuple and pass it into the second function.

Here is how we can use it

x = 10
out = inverse(x)
out2 = map(out, inc)
print(out2) # (True, 1.1)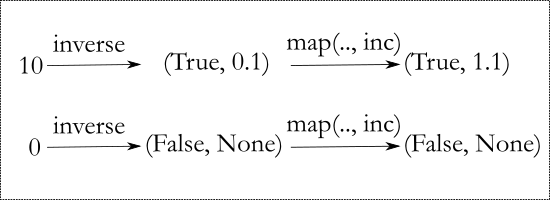

The Maybe monad

Let us give names to everything that we have done so far.

We changed the signature of the inverse function to wrap the output in a tuple and store True / False alongside it. In functional programming, this structure of storing additional context with the output value is called a Monad.

This particular monad is called the Maybe monad and is used to denote when the data might have a value, or it might be empty.

The Maybe monad can be in one of two states

• Nothing which represents an empty state
• Just(x) which represents a state containing the value x

The map function will take a Maybe value and apply a function to the value. If the monad is in the Nothing state then map returns Nothing.If the value is Just(x) then it applies the function to x and wraps the answer with Just.

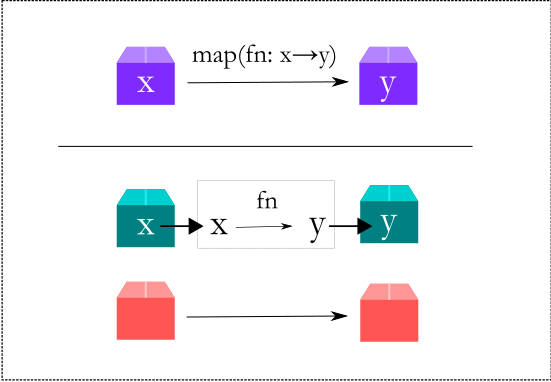
Let us rewrite our code using above terminology. We could continue using tuples as before, but it's cleaner to create classes like this:

class Nothing:
    def map(self, fn):
        return self
        
    def __str__(self):
        return "Nothing()"

class Just:
    def __init__(self, val):
        self.val = val

    def map(self, fn):
        return Just(fn(self.val))
        
    def __str__(self):
        return f"Just({self.val})"

We change inverse  to use these classes instead of wrapping with tuples

def inverse(x):
    if x == 0:
        return Nothing()
    return Just(1/x)

Then we can compose them together as before.

x = 10
out = inverse(x).map(inc)
print(out) # Just(1.1)

The flatmap method

In the example above, we composed with the inc function via the map method.

inc is a normal function in the sense that it takes an ordinary value as input and returns a value as output – there is no monad involved in this function.

Compare this to inverse which returns a monad.

Let us now see what happens if we compose inverse with itself – we want to take a number x then calculate the inverse of x, and then again take the inverse of the result.

The first attempt might be something like this

out = inverse(x).map(inverse)

Lets follow the code execution here for x = 10.

For x = 10, the inverse function will return Just(0.1).

Then we do .map(inverse), so line 12 will execute and it will call fn(self.val) and wrap the result with Just.

fn(self.val) in this case is inverse(0.1) which will return Just(10). And that result will be wrapped with Just, so the final answer will be Just(Just(10))

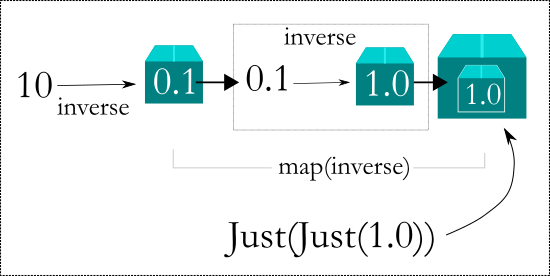
You see the problem here. When the function to compose itself returns a Just(x), the map method will wrap it with a Just once more, leading to a double wrapping.

To avoid this, we introduce another method flatmap. The goal of flatmap is to "flatten" the double wrapping and make it a single wrap again.

Here is how flatmap should work

• In the case that the monad is in the Nothing state, then flatmap should return Nothing() without continuing the computation.
• If it is Just(x) then flatmap takes x and passes it to the next function. flatmap returns the output of the function as it is without wrapping it, since the function itself returns a monad.

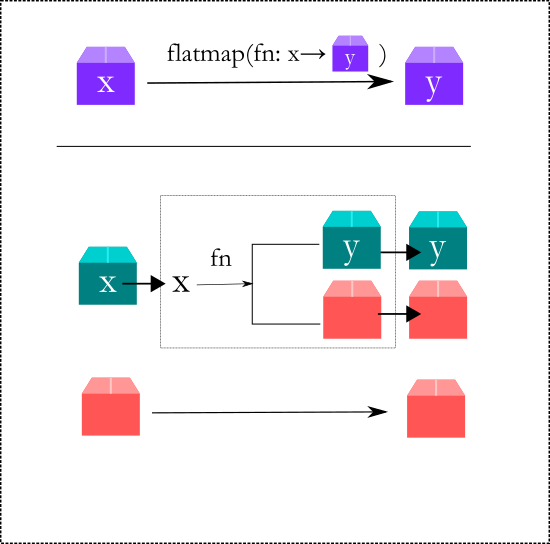
This is what we get when we implement the steps above

class Nothing:
    def map(self, fn):
        return Nothing()

    def flatmap(self, fn):
        return Nothing()
        
    def __str__(self):
        return "Nothing()"

class Just:
    def __init__(self, val):
        self.val = val

    def map(self, fn):
        return Just(fn(self.val))

    def flatmap(self, fn):
        return fn(self.val)
        
    def __str__(self):
        return f"Just({self.val})"

Now the following composition will work

x = 10
out = inverse(x).flatmap(inverse)
print(out) # Just(10.0)

Combining map and flatmap

We can now combine map and flatmap to do any kind of composition.

Suppose we want to compose inverse → inc → inverse → inc the code is simply this

x = 1
out = inverse(x).map(inc).flatmap(inverse).map(inc)
print(out) # Just(1.5)

x = -1
out = inverse(x).map(inc).flatmap(inverse).map(inc)
print(out) # Nothing()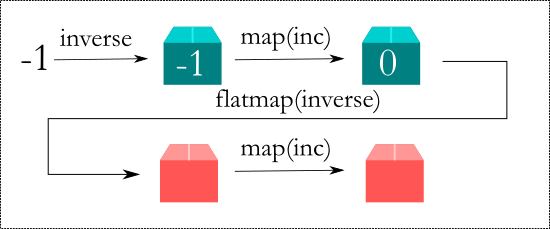

Whenever we compose a normal function like inc we will use map and when we compose with a function that itself returns a Maybe then we use flatmap to do the composition.

Notice something else?

Even though inverse might fail, we don't need to have any if/else checks anywhere in the composition. We just compose the functions together and if the complete composition succeeds then we will get Just(x) as the output. If any part of the composition fails, we get Nothing as the output.

This code using monads is very easy to read.

Summary

In this article, we saw how to use the Maybe monad to compose together functions which might fail. The resulting code is very clean and easy to read, with no need to put if/else checks all over the place.

In the next article, we will see how we can apply the Maybe monad to the robot kata.