Python Decorators

You come across decorators when working in many frameworks. For example, here is some code from Flask

@app.route("/")
def hello_world():
    return "<p>Hello, World!</p>"

And this one is from SQLAlchemy

@compiles(BINARY, "sqlite")
def compile_binary_sqlite(type_, compiler, **kw):
    return "BLOB"

In the code snippets above, @app.route and @compiles are decorators. But what really are they?

Decorators

Decorators are functions that take one function as input and return another function as output.

Let us read that again. Decorators are

• functions that
• take a function as input
• return a function as output

In other words, decorators are just higher order functions, a concept that we are already acquainted with.

What is all that @ stuff then? That is just a syntax sugar to make it easier to apply decorators. We will come back to that syntax later. For now, let us take a look at an example.

Decorator example

In the example below we are going to write some code to to solve a quadratic equation. Don't worry if you are not familiar with quadratic equations, all we care about is the formula. This is the formula

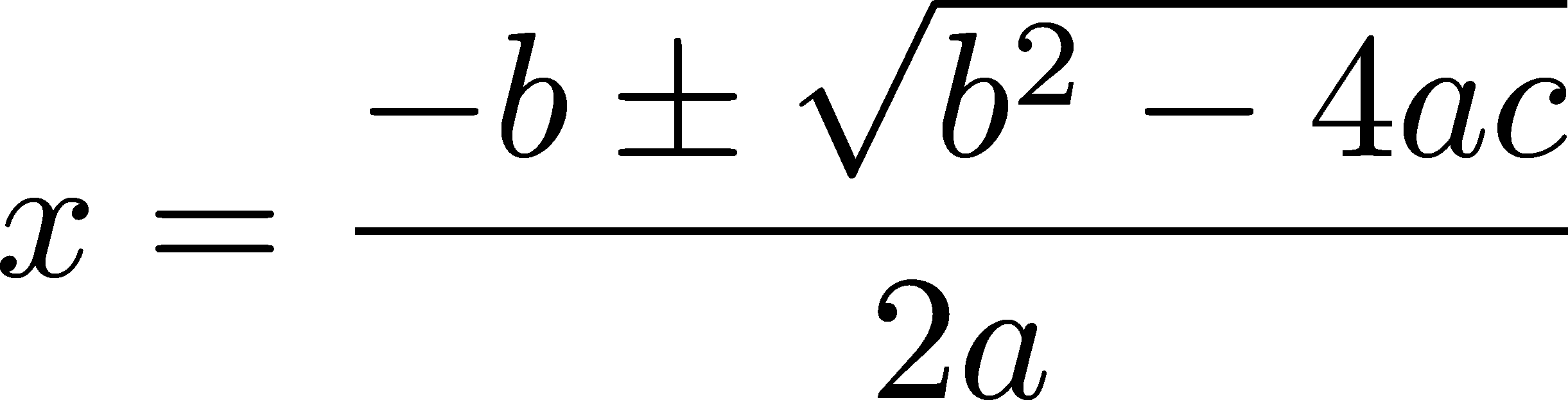
and below is the implementation for a = 5, b = 6 and c = 1. The correct answer is -0.2. Note that in this implementation I have used function call syntax instead of using the operator syntax (ie add(a, b) instead of a + b etc)

from operator import add, mul, sub, truediv
from math import sqrt, pow

a = 5
b = 6
c = 1
result = truediv(add(-b, sqrt(sub(pow(b, 2), mul(4, mul(a, c))))), mul(2, a))
print(result)

Let us say something is going wrong with this code, and we want to log the flow so that we can follow the calculation step by step. We want something like this

def add_log(*args, **kwargs):
    print(f"Calling add with params {args}, {kwargs}")
    out = add(*args, **kwargs)
    print(f"result of add = {out}")
    return out

If we use add_log instead of add in calculating the formula then it will print out the arguments before doing the add operation and also the result after doing the operation. We now need something similar for mul, sub, truediv, sqrt and pow. Also if there were any errors, we would like to log that too.

How can we generalise add_log for all these other operations? You probably already know the answer–higher order functions.

Here is the implementation

def enable_logging(fn):
    def inner(*args, **kwargs):
        try:
            print(f"calling {fn.__name__} with params {args, kwargs}")
            out = fn(*args, **kwargs)
            print(f"result of {fn.__name__} = {out}")
            return out
        except:
            print("got error")
            raise
    return inner

The enable_logging function takes any function fn as input and returns the function inner as output. You can see that inner is just a generalised version of add_log.

If we give add as the input to this function, we will get add_log as the output.

add_log = enable_logging(add)

Similarly we can pass in mul, pow and all the others to this higher order function and get their logging versions.

There is still a problem: we need to modify the result calculation and everywhere we are using add we need to change it to add_log. Only then will we get the logging functionality.

We can get around this by assigning the output of enable_logging back to the same variable name. Now anytime the add function is called, it will actually call the logging version. We don't need to change the result calculation any more

add = enable_logging(add)

Remember that function names are just variables, and you can reassign them just like any other variable.

With that change, we can now do this

add = enable_logging(add)
mul = enable_logging(mul)
sub = enable_logging(sub)
truediv = enable_logging(truediv)
sqrt = enable_logging(sqrt)
pow = enable_logging(pow)

a = 5
b = 6
c = 1
result = truediv(add(-b, sqrt(sub(pow(b, 2), mul(4, mul(a, c))))), mul(2, a))
print(result)

and we get the logs

calling pow with params ((6, 2), {})
result of pow = 36.0
calling mul with params ((5, 1), {})
result of mul = 5
calling mul with params ((4, 5), {})
result of mul = 20
calling sub with params ((36.0, 20), {})
result of sub = 16.0
calling sqrt with params ((16.0,), {})
result of sqrt = 4.0
calling add with params ((-6, 4.0), {})
result of add = -2.0
calling mul with params ((2, 5), {})
result of mul = 10
calling truediv with params ((-2.0, 10), {})
result of truediv = -0.2

Notice that we don't need to change the code where we are calculating result. When we pass the functions through enable_logging then we will get the logs. If we use the base functions without passing through enable_logging we get the regular functionality.

Functions like enable_logging are called decorators because they "decorate" the original function with some additional functionality. Here we are adding logging functionality to the base function. Decorators allow us to separate aside the code for these types of functionality from the actual business logic that we are trying to calculate. We can easily add in the decoration, or remove it, without touching the main logic. We can add it for some functions, but not for others. It is very flexible.

Static and dynamic decoration

Let us start with this function

def do_something():
    print("doing calculation")

If we want to enable logging on this function, then we need to transform it through enable_logging.

do_something = enable_logging(do_something)

Python provides a shortcut to do the above step

@enable_logging
def do_something():
    print("doing calculation")

Thats what the @ syntax does. You put @decorator above the function and it will pass in the function below through the decorator function and replace the function variable name to point to the output of the decorator.

This application of the decorator is static. If you want to remove the decorator, you have to go to the code and remove the @enable_logging line.

What if you want to enable a decorator dynamically at runtime?

To do that, you just pass the function through the decorator yourself instead of using the @ syntax. The code below will enable or disable logging based on the value of the logging variable.

from operator import add, mul, sub, truediv
from math import sqrt, pow

logging = input("Do you want logging? [y/n] ")
if logging.lower() == "y":
    add = enable_logging(add)
    mul = enable_logging(mul)
    sub = enable_logging(sub)
    truediv = enable_logging(truediv)
    sqrt = enable_logging(sqrt)
    pow = enable_logging(pow)

a = 5
b = 6
c = 1
result = truediv(add(-b, sqrt(sub(pow(b, 2), mul(4, mul(a, c))))), mul(2, a))
print(result)

Try it out! If the user inputs y then the logs will be shown. Otherwise the logs will not be displayed.

Notice how clean the code is? The business logic part which calculates the result remains as it is. You can enable and disable logging without touching that part of the code. That is the power of decorators and higher order functions!

Hopefully that gives you a better idea of decorators, what they are, and how they work. And if you have been following along from the beginning of this series, you also have a solid conceptual foundation to understand decorators. There are many more things you can do with decorators, which we will look at in a future article.